Comment trader avec Fibonacci ?

Le nombre d’or est entouré de mystères et a engendré de nombreuses théories dans des domaines très différents. Ainsi, ce nombre peut être retrouvé dans les pyramides de Khéops (rapport de sa hauteur par sa demi-base), dans le Parthénon (qui s’inscrit dans un rectangle d’or) ou encore dans la nature (au sein de nombreuses formes biologiques-, mais également dans l’art. Ce nombre est à l’origine de la suite de Fibonacci, tout aussi mystérieuse. À titre d’exemple, on peut remarquer que le nombre de pétales des fleurs correspond souvent à un nombre de la suite de Fibonacci : 3 (les lis), 5 (les boutons d’or), 8 (le delphium), 13 (le souci), 21 (les chicorées), 34 (les marguerites) ou encore 55 (les tournesols).

La suite de Fibonacci est très largement utilisée en tant qu’indicateur boursier et permet de déterminer des niveaux de support et de résistance sur la base du précédent mouvement, haussier ou baissier. Avant de nous intéresser à la suite de Fibonacci et à son application dans le trading à travers notamment les retracements, nous allons aborder brièvement le nombre d’or et sa présence dans les mathématiques et la géométrie.

Le nombre d’or dans les mathématiques et la géométrie

En mathématiques, le nombre d’or est 1.61803398…avec pour symbole Փ (phi)

Ce nombre est la seule solution positive de l’équation x² = x + 1, et est égal à :

Փ = x2.

Cette relation présente des caractéristiques uniques, dont notamment :

Փ²=Փ+1 et 1/Փ=Փ-1

Le nombre d’or est apparu pour la première fois dans le livre « Eléments » d’Euclide, ce dernier cherchant à partager un segment AC par un point B tel que AB/BC = AC/AB, ce qui nous renvoie à l’équation précédente x²- x -1 = 0.

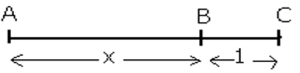
Le rectangle d’or

Le nombre d’or est également présent en géométrie et il existe un rectangle très particulier appelé rectangle d’or. Le rapport entre la longueur et la largeur d’un rectangle d’or est égal au nombre d’or.

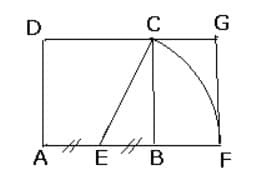
Pour que le rectangle ADGF soit un rectangle d’or, AF/AD doit être égal à √5)/2

Un tel rectangle peut être construit sur la base d’un carré ABCD de côté 1 avec “E”, milieu du côté AB. Il suffit de tracer un arc de cercle de centre E et de rayon EC, cet arc de cercle coupe (AB) en F, et nous obtenons le point G, permettant de former un rectangle ADGF.

Le triangle isocèle

Le nombre d’or peut également être trouvé dans un triangle isocèle en C avec des angles A et B à 36°

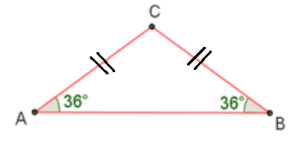
Dans ce cas là, BC / AC = Փ

Le pentagone régulier

Փ peut être retrouvé dans un pentagone régulier (polygone avec 5 côtés égaux), en divisant une diagonale par un côté.

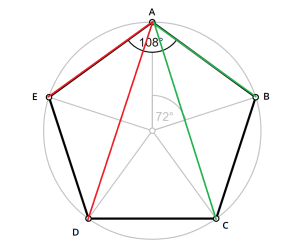
Ici AD / AE = √5)/2  ou AC / AB = √5)/2

Le décagone régulier

Enfin, un décagone régulier (polygone avec 10 côtés égaux) présente lui aussi le nombre d’or en divisant le rayon du cercle contenant le décagone régulier par l’un de ses côtés.

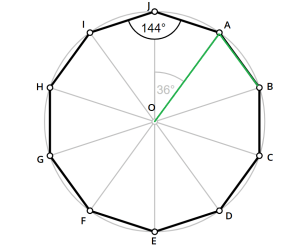
Dans ce cas, 0A / AB = √5)/2

Après avoir survolé le nombre d’or dans les mathématiques et la géométrie, nous allons détailler ce qui lie ce nombre d’or et le monde boursier, la suite de Fibonacci.

Suite de Fibonacci : qu’est-ce que c’est ?

La suite de Fibonacci a été inventée par un mathématicien italien, Leonardo de Pise ou Leonardo Fibonacci, largement connu pour avoir introduit en Europe les nombres indo-arabe à travers un traité sur les calculs et la comptabilité. Les deux premiers termes de cette suite sont 0 et 1 et permettent de déduire les termes suivants, chaque terme successif étant la somme des deux précédents.

Ainsi : 0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, 5 + 8 = 13 et ainsi de suite.

La suite de Fibonacci commence donc par : 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377…

Les propriétés de cette suite sont nombreuses dont notamment le rapport entre un terme et le précédent proche du nombre d’or (pour rappel, 1.61803398…).

En effet, 8 / 5 = 1,6; 13 / 8 = 1,625; 21 / 13 = 1,615; 34 / 21 =  1,619 …

Retracements de Fibonacci : qu’est-ce que c’est ?

Les niveaux de retracement de Fibonacci sont presque tous issus de cette suite, seul le retracement de 50 % ne provient pas de cette suite.

La division d’un terme par le terme suivant est proche de 0,618, soit 61,8 % en ne tenant pas compte des quatre premiers termes. Par exemple : 1 / 1 = 1 ; 1 / 2 = 0,5 ; 2 / 3 = 0,67 ; 3 / 5 = 0,60 ; 5 / 8 = 0,625 ; 8 / 13 = 0,615 ; 13 / 21 = 0,619. Il convient de noter que les résultats successifs fluctuent autour de 0,618 dans un premier supérieur puis inférieur avec une amplitude qui se réduit tout le long de la série des rapports.

La division d’un terme par le précédent est à peu près égale à 1,618 ou son inverse de 0,618.  Par exemple : 13 / 8 = 1,625 ; 21 / 13 = 1,615 ; 34 / 21 = 1,619. Plus les termes de cette division sont élevés, plus le résultat est proche de 1,618 ou de 0,618

En alternant le rapport de deux termes successifs, on obtient 2,618 ou son inverse 0,382. Par exemple 13 / 34 = 0,382 et en inversant le rapport, 34 / 13 = 2,615

En divisant un terme par le deuxième terme à sa droite, on obtient 0,382 soit 38,2 %.

Enfin, en divisant un terme par le 3^ème terme à sa droite, on obtient 0,236, soit 23,6 %.

Le plus simple reste de se souvenir que chaque terme représente environ 61,8 % du suivant et 38,2 % du second, puis 23,6 % du troisième. Nous obtenons ainsi les retracements de Fibonacci de 23,6 %, 38,2 % et 61,8 %; auxquels nous ajoutons le retracement de 50 % et le nombre d’or de 161,8 % (1.61803398…).

Comment utiliser les retracements de Fibonacci en Bourse ?

Maintenant que nous comprenons l’origine des retracements de Fibonacci, nous allons nous intéresser à la partie graphique afin de les intégrer aux cours boursiers et d’en constater l’utilité.

L’idée qui se cache derrière les retracements de Fibonacci est que les cours boursiers retracent constamment une partie du mouvement précédent qui s’inscrit dans la tendance de fond.

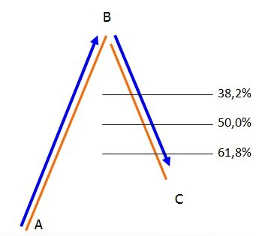
Un mouvement haussier AB sera retracé d’un certain pourcentage par un mouvement BC, avant la construction d’une nouvelle jambe haussière.

Dans une tendance haussière, les retracements de Fibonacci vont de 0 % au niveau du pic, à 100 % à la base du mouvement haussier. Au milieu se trouvera le point médian, ou retracement de Fibonacci de 50 %. Afin d’appliquer les retracements à un graphique boursier, il faut sélectionner l’outil « retracement de Fibonacci”, et relier le point bas au point haut en cas de tendance haussière.

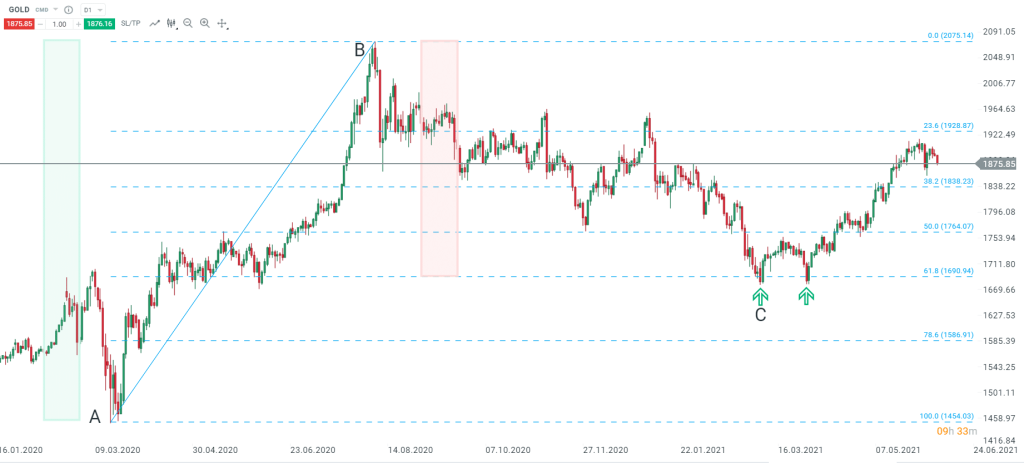
L’or (GOLD) en données journalières avec retracements de Fibonacci. Source : xStation5 de XTB

Le graphique ci-dessus met en évidence la force du retracement de 61,8 % qui a permis de stopper la baisse du métal jaune, entraînant une formation en double creux, figure chartiste indiquant un retournement haussier.

En cas de tendance baissière, afin de placer les retracements de Fibonacci, il faut relier le point haut au point bas comme ci-dessous.

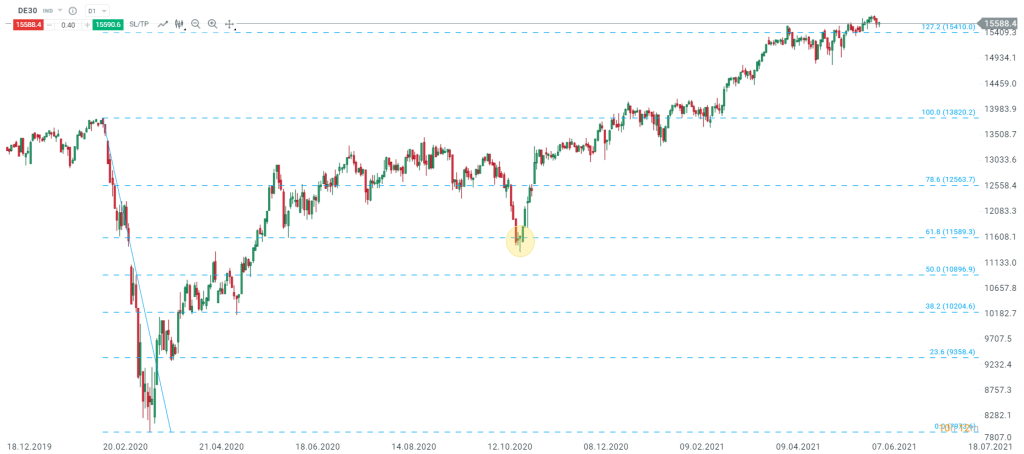
Le DAX (DE30) en données journalières avec retracements de Fibonacci. Source : xStation5 de XTB

Ici nous pouvons constater à nouveau que le retracement de Fibonacci de 61,8 % issu de la baisse intervenue lors de la propagation du COVID-19 fin février 2020 a permis de stopper la baisse d’octobre 2020. Dans cet exemple, le mouvement baissier a été retracé dans son intégralité et la hausse se poursuit. Les cours évoluent aux alentours de l’expansion de Fibonacci de 127,2 %. Nous aborderons les expansions par la suite, mais avant cela nous allons nous intéresser à l’intérêt des retracements de Fibonacci dans le trading.

Comment utiliser l’indicateur de Fibonacci en trading ?

Les retracements de Fibonacci peuvent être utilisés en trading pour générer des signaux d’achat ou de vente. Par exemple, une cassure à la baisse du retracement de Fibonacci de 61,8 % pourrait constituer un signal baissier. Cependant, il est fortement conseillé de confirmer de tels signaux à l’aide d’autres indicateurs, de figures chartistes (exemple du double creux se formant au niveau du retracement de 61,8 % pour le graphique journalier sur l’or), ou de configurations de chandeliers japonais.

Les retracements de Fibonacci sont très utilisés afin de déterminer des niveaux de stop-loss ou d’objectif. En revanche, il serait plus judicieux de laisser une certaine marge dans le cas des stop-loss, afin d’éviter d’enclencher ce dernier avant une reprise des cours dans le sens opposé.

L’avantage des retracements de Fibonacci par rapport à d’autres indicateurs est que ses niveaux sont statiques, contrairement aux moyennes mobiles. La nature statique de ces niveaux permet une identification rapide et facile, mais également d’anticiper de réagir en conséquence lors de tests. Ces niveaux sont des points d’inflexion où l’on s’attend à une réaction, soit un renversement, soit une cassure.

En somme, les retracements de Fibonacci sont à considérer comme des niveaux de support et de résistance. Afin de limiter les risques, il convient de se positionner dans le sens de la tendance majeure. Ainsi, en cas de tendance haussière, un test suivi d’un rebond sur le retracement de 61,8 % pourrait être un point d’achat optimal. C’est le cas du graphique sur l’or en données journalières que nous avons abordé précédemment.

L’expansion de Fibonacci en cas de records historiques

Dans le cas d’une tendance haussière, les retracements de Fibonacci appliquent des pourcentages à un repli, les extensions ou expansions de Fibonacci quant à eux appliquent des pourcentages à un mouvement dans la direction de la tendance. Les expansions de Fibonacci sont 127,2 % 161,8 % 261,8 % et 423,6 %. Ils représentent des niveaux au-delà du niveau de prix du dernier sommet (ou creux dans le cas d’une tendance baissière majeure).

Ces niveaux peuvent être utiles pour placer des objectifs et sont un outil incontournable lorsque les cours évoluent sur des records historiques. En effet, des niveaux records n’ont pas d’équivalent dans l’historique des cours, il est donc très difficile de déterminer les prochaines résistances. Seuls les seuils psychologiques (chiffres ronds) pourront être considérés comme potentielles résistances. L’exemple ci-dessous en données hebdomadaires illustre parfaitement ces propos.

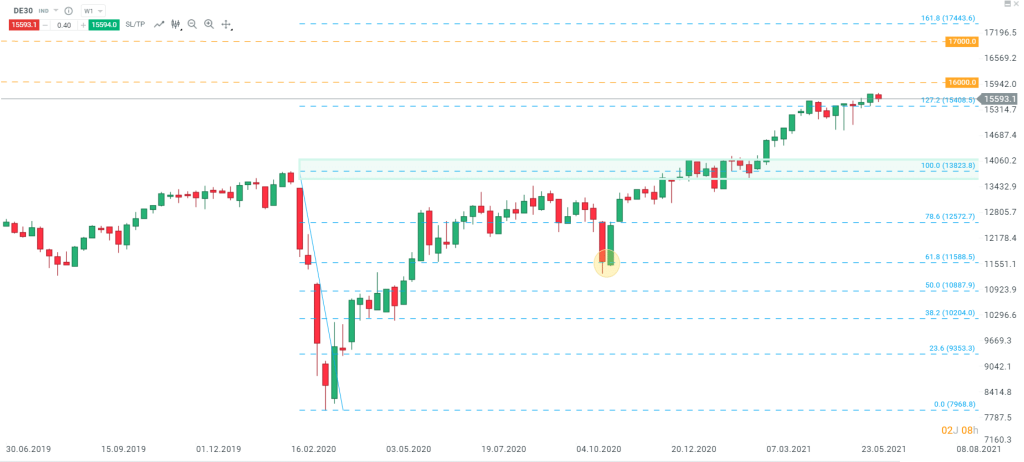
Le DAX (DE30) en données hebdomadaires avec retracements et extensions de Fibonacci. Source : xStation5 de XTB

Les limites des retracements de Fibonacci

Bien que les niveaux de retracement indiquent où le cours pourrait trouver un support ou une résistance, il n’y a aucune certitude que le prix soit stoppé sur un de ces niveaux. C’est pourquoi d’autres signaux de confirmation sont souvent utilisés, à travers des indicateurs ou oscillateurs, voire en examinant le comportement des cours au contact des retracements. Il sera plus judicieux d’attendre la clôture du chandelier japonais et de surveiller l’ouverture du prochain chandelier avant de conclure à une cassure.

Un argument en défaveur des retracements de Fibonacci est que ces derniers sont si nombreux que les cours sont susceptibles de se retourner au contact de l’un d’eux. Afin de compléter l’analyse à l’aide de Fibonacci, il est donc recommandé de tracer les lignes de tendances. En effet, un retracement de Fibonacci qui se confond avec une ligne de tendance aura de fortes chances de résister au cours et de ne pas céder.

Source des images : Freepik

Toutes nos informations sont, par nature, génériques. Elles ne tiennent pas compte de votre situation personnelle et ne constituent en aucune façon des recommandations personnalisées en vue de la réalisation de transactions et ne peuvent être assimilées à une prestation de conseil en investissement financier, ni à une incitation quelconque à acheter ou vendre des instruments financiers. Le lecteur est seul responsable de l’utilisation de l’information fournie, sans qu’aucun recours contre la société éditrice de Cafedelabourse.com ne soit possible. La responsabilité de la société éditrice de Cafedelabourse.com ne pourra en aucun cas être engagée en cas d’erreur, d’omission ou d’investissement inopportun.